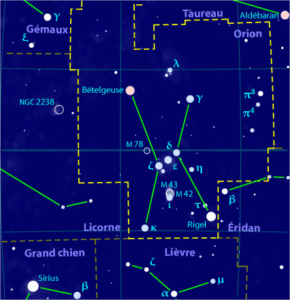
La constellation d’Orion et ses limites actuelles, CC BY-SA 3.0, via Wikimedia Commons
Sommaire
- Introduction
- Avant les Grecs : l’astronomie mésopotamienne
- Aux origines : Homère, Hésiode, le skyphos d’Halai
- La révolution du VIe s. : Thalès, Anaximandre, Pythagore
- Le Ve s. : Philolaos de Crotone, Archytas de Tarente, Euctémon
- Le IVe s. : Eudoxe de Cnide, Aristote, Aratos, Héraclide du Pont, Callippe de Cyzique
- Le IIIe s. : Aristarque de Samos, Ératosthène de Cyrène
- Le IIe s. : Hipparque, Claude Ptolémée
- Les instruments de l’astronomie
- Bibliographie
Introduction
En ces temps pré-industriels, où aucune pollution d’origine humaine ne venait troubler le spectacle de la voute céleste, la contemplation des étoiles devait s’imposer dès le plus jeune âge aux enfants grecs, qu’ils vivent en ville où à la campagne, et ce depuis la préhistoire. Très vite, il apparut nécessaire de s’orienter dans la foule des astres : l’on s’aperçut vite que la position des astres entre eux était stable, et l’on procéda à des regroupements, plus ou moins arbitraires, que l’on nomma les constellations ; on leur attribua des noms, en rapport avec leur forme, l’Ourse, le Chariot… et l’on rattacha ces constellations aux mythes et aux héros… Ainsi naquit sans doute une première carte du ciel. Ces appellations, purement conventionnelles, frappent par leur durée : la plupart des constellations, ainsi définies, ont gardé leur nom jusqu’à nos jours.
Mais si les constellations restaient stables – d’où leur nom de « sphère des fixes », leur emplacement variait, à la fois dans la durée d’une nuit, entre le coucher et le lever du soleil, dans celle de l’année, en fonction des saisons, et enfin selon l’endroit où l’on se trouvait : les étoiles offrirent à l’homme sa première horloge nocturne (pour le jour, le soleil y pourvoyait), son premier calendrier, et un repère géographique, peu utile au paysan, mais essentiel au voyageur et surtout au navigateur.
Telle était donc la représentation du ciel : au centre, la Terre, immobile mais animée d’un mouvement de rotation sur elle-même autour d’un axe ; autour d’elle, la sphère céleste, divisée en deux hémisphères : l’un, au Nord, visible ; l’autre, au Sud, invisible. Sur cette sphère, plusieurs cercles, sur lesquels se trouvent fixées les étoiles : l’Équateur, les deux tropiques, le Zodiaque, plus tard le cercle arctique, visible, et antarctique, invisible. Il faut enfin ajouter le Soleil, la Lune, et cinq planètes ainsi nommées (« les Errantes ») parce que dans la perspective géocentrique, leur course semblait aléatoire et imprévisible (la sixième, Uranus, invisible à l’œil nu, sera découverte en 1781 par William Herschel, et la septième, Neptune, grâce à des calculs mathématiques, par Le Verrier en 1846)…
Avant les Grecs : l’astronomie mésopotamienne
Rien ne devait être plus angoissant pour les peuples antiques que la soudaine disparition du Soleil lors des éclipses ; or très vite, l’on s’aperçut que ce phénomène, riche en présages de toutes sortes, se reproduisait à intervalles plus ou moins réguliers.
Les Babyloniens, puis les Chaldéens, furent les premiers à consigner dans des tables ces récurrences, qui pouvaient leur permettre de prévoir les éclipses. Puis, à force de noter dans leurs éphémérides les mouvements de la lune et des planètes, ils en déduisirent les phases de la lune.
À chaque planète, ils parvinrent à associer deux cycles :
- la révolution zodiacale : temps entre deux passages par la même position par rapport au Soleil ;
- la révolution synodique : le temps entre deux passage par la même position par rapport aux étoiles fixes.
Ils en déduisirent la Grande Année : « période dans laquelle toutes les planètes, après avoir effectué un nombre entier de révolutions synodiques, se retrouvent à la même place dans la voute céleste » (P. Brémaud, Le Dossier Pythagore, p. 256).
Cependant, les Chaldéens en étaient restés au constat, sans parvenir à expliquer quelles lois permettraient d’expliquer ces mouvements des planètes. Il revenait aux Grecs de trouver la théorie de ces mouvements.
Aux origines : Homère, Hésiode et le skyphos de Halai
Homère
Sur Homère : voir ici.
Homère est le premier auteur grec dont nous ayons connaissance ; on peut le dater du IXe ou du VIIIe s. av. J-C.
Il mentionne les astres dans deux passages de son œuvre, l’un dans l’Iliade, l’autre dans l’Odyssée.
L’Iliade, chant XVIII, v. 481-489.
Achille, qui vient d’apprendre la mort de son ami Patrocle, veut reprendre le combat aux côtés des Grecs, après sa « grève » consécutive à sa dispute avec Agamemnon. Sa mère obtient d’Héphaïstos, le dieu forgeron, des armes et en particulier un bouclier dont la description constitue l’une des premières « ecphrasis » de la littérature occidentale.
Le passage sur les constellations est le suivant :
[…] αὐτὰρ ἐν αὐτῷ
ποίει δαίδαλα πολλὰ ἰδυίῃσι πραπίδεσσιν.
Ἐν μὲν γαῖαν ἔτευξ᾽, ἐν δ᾽ οὐρανόν, ἐν δὲ θάλασσαν,
ἠέλιόν τ᾽ ἀκάμαντα σελήνην τε πλήθουσαν,
ἐν δὲ τὰ τείρεα πάντα, τά τ᾽ οὐρανὸς ἐστεφάνωται, 485
Πληϊάδας θ᾽ Ὑάδας τε τό τε σθένος Ὠρίωνος
Ἄρκτόν θ᾽, ἣν καὶ Ἄμαξαν ἐπίκλησιν καλέουσιν,
ἥ τ᾽ αὐτοῦ στρέφεται καί τ᾽ Ὠρίωνα δοκεύει,
οἴη δ᾽ ἄμμορός ἐστι λοετρῶν Ὠκεανοῖο.Il y représente, par son art ingénieux, beaucoup de motifs artistiques. Il y plaça la terre, le ciel, la mer, et le soleil infatigable et la pleine lune, et toutes les constellations dont se couronne le ciel, les Pléiades, les Hyades et la force d’Orion et l’Ourse, que l’on appelle aussi du surnom du Chariot, qui tourne sur elle-même et observe Orion, et qui est privée des bains de l’Océan.
L’Odyssée, chant V, v. 269-277.
Dans ce passage du chant V, la mention des constellations est directement liée à la navigation. Ulysse vient de s’embarquer sur le radeau qu’il a construit, sur les conseils de Calypso, pour quitter l’île de celle-ci et regagner Ithaque. Voici le texte :
Γηθόσυνος δ᾽ οὔρῳ πέτασ᾽ ἱστία δῖος Ὀδυσσεύς.
Αὐτὰρ ὁ πηδαλίῳ ἰθύνετο τεχνηέντως 270
ἥμενος, οὐδέ οἱ ὕπνος ἐπὶ βλεφάροισιν ἔπιπτεν
Πληιάδας τ᾽ ἐσορῶντι καὶ ὀψὲ δύοντα Βοώτην
Ἄρκτον θ᾽, ἣν καὶ ἄμαξαν ἐπίκλησιν καλέουσιν,
ἥ τ᾽ αὐτοῦ στρέφεται καί τ᾽ Ὠρίωνα δοκεύει,
οἴη δ᾽ ἄμμορός ἐστι λοετρῶν Ὠκεανοῖο· 275
τὴν γὰρ δή μιν ἄνωγε Καλυψώ, δῖα θεάων,
ποντοπορευέμεναι ἐπ᾽ ἀριστερὰ χειρὸς ἔχοντα.Joyeux, le divin Ulysse déploya ses voiles au vent favorable. Alors, assis il dirigeait habilement son navire avec le gouvernail, et le sommeil ne tombait pas sur ses paupières, à lui qui observait les Pléiades, et longtemps après le Bouvier et l’Ourse, que l’on appelle aussi du surnom du Chariot, qui tourne sur elle-même et observe Orion, et qui est privée des bains de l’Océan ; c’est elle qu’il doit, selon les révélations de Calypsô, divine entre les déesses, avoir à main gauche en navigant.
Ici, la connaissance des étoiles est explicitement mise en relation avec les nécessités de la navigation nocturne. On y retrouve les mêmes constellations que dans l’Iliade, les Pléiades, l’Ourse autrement appelée Chariot, et Orion. Mais en plus, elles indiquent un cap : en partant d’Ogygie, l’île de Calypso, en direction d’Ithaque – donc vers l’Est – il faut garder l’Ourse à bâbord.
Cette remarque a permis à Jean Cuisenier de déterminer où pouvait se trouver la mystérieuse Ogygie. Il suffit en effet d’imaginer la route en sens inverse, en partant d’Ithaque : il faudrait alors garder constamment l’Ourse à droite, c’est-à-dire à tribord, sur une distance d’environ 1300 milles.
« Qui part à la recherche de l’homérique Ogygie doit donc […] tenir la côte africaine à main gauche, l’Ourse à main droite, et avancer ainsi loin, toujours plus loin, pendant des jours et des jours, une dizaine peut-être, en longeant la côte d’Afrique jusqu’à prendre terre aux parages évoqués dans le mythe sous les noms d’Océan et d’Atlas » (Jean Cuisenier, Le Périple d’Ulysse, éditions Fayard 2003, p. 335).
On aboutirait alors non loin du détroit de Gibraltar, autrement dit les « colonnes d’Hercule », sur la côte marocaine, près de l’enclave espagnole de Ceuta, plus précisément une petite île située au pied du Mont aux Singes, sommet le plus élevé de cette côte : l’île del Perejil, ou « île du Persil ». Cette île correspond assez bien à la description de l’Odyssée :
- par sa végétation (cèdres, aulnes, et le fameux persil sauvage – « tout autour fleurissaient de douces prairies de violettes et de persil », v. 73–) qui constitue la riche prairie de la déesse ; si aujourd’hui elle apparaît aride et quasi déserte, des témoignages anciens prouvent qu’elle était, dans l’antiquité, couverte de forêts et de prairies luxuriantes.
- elle contient aussi une vaste grotte, et une série de cascades peut figurer les quatre sources dont parle Homère…

L’île de Perejil (Leila) vue de la côte africaine –
eForge, CC BY 3.0 , via Wikimedia Commons
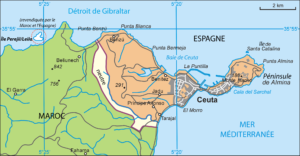
Carte montrant le nord du Maroc et l’enclave espagnole de Ceuta, incluant l’îlot Persil (en haut à gauche). Domaine public via Wikimedia Commons. Pour agrandir, cliquer sur l’image.
Conclusion : Homère et l’astronomie
Les constellations citées par Homère sont assez peu nombreuses, mais essentielles :
- L’Ourse est la plus importante, notamment parce qu’elle ne se couche jamais dans l’Océan et reste donc constamment visible la nuit. Elle est aussi la plus anciennement connue, dans l’ensemble de l’hémisphère Nord : on retrouve cette figure chez les Amérindiens, ce qui ne signifie pas une relation quelconque avec l’Europe, mais révèle l’importance de cet animal dans la vie et l’imaginaire de l’ensemble de ces peuples.
L’Ourse est aussi nommée « le Chariot » : c’est un emprunt à l’astronomie mésopotamienne. - Les Pléiades, une constellation de sept étoiles visibles (et une quantité d’autres invisibles à l’œil nu), dont nous verrons chez Hésiode l’importance pour le calendrier agricole ;
- Les Hyades ;
- Le Bouvier ;
- et surtout Orion, ou « la Force d’Orion » que l’on retrouvera également chez Hésiode. Ce personnage mythologique, représenté comme un géant, serait également inspiré par l’astronomie mésopotamienne.
Hésiode
- Le poète Hésiode
- La Théogonie
- Les Travaux et les Jours
Le skyphos de Halai (vers 625 av. J-C)
Bibliographie :
- Un article d’Archeolog-home.com
- John T. Barnes, « Asteras Eipein: An Archaic View of the Constellations from Halai », Hesperia n° 83-2, avril-juin 2014, pp. 257-276.
Parmi les plus anciennes représentations picturales du ciel nocturne, figure un skyphos, ou vase à boire de 16,5 cm de haut, à figures noires, daté de 625 av. J-C environ. Il a été trouvé dans un sanctuaire archaïque à Halai, en Locride, en face de l’Eubée, et se trouve aujourd’hui au musée archéologique de Lamia. Il s’agit d’un gobelet de style corinthien, de production locale ; il est orné de trois zones sur fond beige, séparées par des bandes marron-rouge ; la zone centrale présente des animaux, tous tournés vers la gauche : de gauche à droite, un taureau, un serpent, un lièvre ou un petit chien, un grand chien, un scorpion, un dauphin, et le devant d’une panthère ou d’un lion. Entre les animaux, des motifs décoratifs en forme de croix complètent la frise.
Il ne saurait s’agir d’une traditionnelle scène de chasse : le taureau, le serpent, le scorpion et le dauphin ne sauraient s’y intégrer. En revanche, on peut supposer qu’il s’agit d’une représentation des constellations, les croix figurant des étoiles isolées. Cela signifierait que si Hésiode et Homère n’ont cité qu’un petit nombre d’astres, la quasi-totalité des constellations mentionnées par Aratos (IVe s. av. J-C), ou Hygin (Ier s. av. J-C) étaient déjà connues à l’époque archaïque.
Les constellations citées sont les suivantes :
- Le Taureau n’est pas mentionné par les poètes ; ils préfèrent nommer les étoiles qui le composent, les Pléiades et les Hyades ;
- Le Scorpion correspond à Scorpios ;
- Le Dauphin ;
- Le Lion, probablement d’origine babylonienne ou phénicienne, ultérieurement identifié au Lion de Némée, l’un des douze travaux d’Héraklès ;
- Le petit chien est peut-être un lièvre (constellation Lepus) ; peut-être aussi est-il « caniculum », la canicule, autrement dit Sirius, présent chez Hésiode ; celui-ci est aussi appelé « le chien d’Orion ».
- Le grand chien : celui-ci est aussi appelé « le chien d’Orion ». On remarquera que les animaux stellaires forment des groupes : ainsi le géant Orion, et son chien, poursuivant le lièvre…
- Enfin, le Serpent serait l’Hydre de Lerne, autre travail d’Héraklès.
Comme chez Hésiode, la position des constellations au-dessus de l’horizon au moment de leur lever et de leur coucher sert à indiquer les saisons ; on peut distinguer quatre groupes :
- Le Serpent, le Lièvre et le Chien, qui se lèvent à quelques semaines d’intervalle au coucher du soleil, annoncent l’hiver ;
- Le Taureau signifie l’automne ;
- Le Chien et le Scorpion figurent le printemps ;
- Le Dauphin et le Lièvre indiquent l’été.
Le skyphos d’Halai est donc probablement un objet votif offert au temple près duquel il a été découvert. Il y avait probablement une connexion entre la position des constellations et certains événements religieux ; en l’état actuel de nos connaissances, il est difficile d’aller plus loin.
La révolution du VIe s. : Thalès, Anaximandre, Pythagore
Les Milésiens (Thalès, Anaximandre, Anaximène)
Thalès (625-547 av. J-C)
Il aurait été le premier à expliquer les phénomènes naturels de manière strictement rationnelle, sans recours à une intervention divine.
Anaximandre (vers 610 – vers 546 av.J.-C.)
Il s’oppose à Thalès, en donnant pour la première fois une forme géométrique à l’univers : selon lui, la Terre, à qui il attribue la forme d’une colonne tronquée, ne bouge pas, et n’a pas besoin d’un quelconque support, car elle se trouve au centre de l’univers, et par conséquent à équidistance de n’importe quel point de la circonférence de celui-ci : rien ne l’oblige donc à aller dans un sens ou dans l’autre…
Pythagore (580-495 av. J-C) et les Pythagoriciens
Pythagore fut l’un des premiers à formuler l’hypothèse d’une Terre sphérique et non pas plate, mais davantage pour des raisons métaphysiques que pragmatiques : la sphère est considérée comme le solide parfait.
Le Ve s. : Philolaos de Crotone, Archytas de Tarente
Philolaos de Crotone (470-390 av. J.-C.)
Ce disciple de Pythagore fut le premier à proposer, vers 410, un système quasi-héliocentrique : il existerait un « feu central », lieu où se tient Zeus, autour duquel tourne le Soleil, en une année. La Terre, elle, tourne autour de ce feu en 24 h, en lui présentant toujours la même face… Quant à l’Oikoumène, elle se trouve sur la face cachée, ce qui explique que ce feu central nous soit invisible.
Archytas de Tarente (435-347 av. J.-C.)
Euctémon d’Athènes (mort en 432)
Cet astronome, contemporain et collaborateur de Méton, et connu pour ses observations des Solstices, s’est aperçu que les saisons avaient des durées inégales, et que la plus longue d’entre elles était le printemps.
Le IVe s. : Aristote, Eudoxe de Cnide, Aratos, Héraclide
Eudoxe de Cnide (408 (?) -355 (?) av. J-C)
Né dans une famille pauvre à Cnide, en Carie (Asie Mineure), Eudoxe fut à la fois géomètre, médecin, philosophe et astronome. Il aurait voyagé en Perse et en Égypte, peut-être en compagnie de Platon, vers 392 ; puis il serait revenu à Athènes, où il aurait été disciple ou assistant de Platon. Durant le voyage de celui-ci en Sicile, il le remplaça comme scholarque ; puis il fonda, à Cnide, sa propre école, vers 360.
C’est vers 358 qu’il aurait élaboré sa théorie astronomique sur le mouvement des planètes. Selon lui, la Terre est immobile, et les planètes gravitent autour d’elle ; chaque astre est enchâssé dans une sphère centrée sur la Terre et animée d’un mouvement constant.
Les étoiles bougent elles aussi selon Eudoxe, puisque pour lui la Terre est immobile. Elles sont fichées dans une sphère tournant d’Est en Ouest en 24 heures autour de l’axe des pôles de la Terre. Au total « 27 sphères sont nécessaires, dont 1 pour l’ensemble des étoiles, 3 pour la Lune, 3 pour le Soleil et 4 pour chacune des 5 planètes ». Mais ce qui, chez Eudoxe, est purement théorique, prend avec ses successeurs une existence concrète – d’où naîtront les idées d’ « harmonie des sphères », voire de « musique des sphères ».
Cette théorie avait été ébauchée par Pythagore ; et elle sera reprise par Platon dans le Timée, par Aristote dans le Traité du Ciel, et surtout par Claude Ptolémée qui la complètera : elle fera alors autorité jusqu’à Copernic.
Eudoxe de Cnide fut aussi le premier à calculer la révolution de la terre, en 365 jours 1/4, ce qui est très proche de sa valeur réelle ; il établit aussi une liste de 44 constellations, dont la moitié proviendrait de l’astronomie mésopotamienne. Il serait aussi l’inventeur du cadran solaire appelé « araignée » : un cadran horizontal, un style vertical, et des lignes horaires ondulées évoquant les pattes d’une araignée.
Héraclide du Pont (388-310 av. J-C)
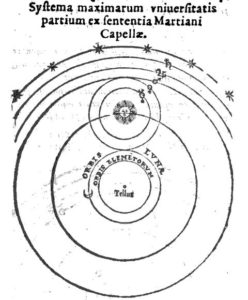
Le système d’Héraclide, transmis par Martianus Capella et dessiné par Valentin Naboth. Domaine public via wikimedia Commons
Cet autre disciple de Platon aurait – et il faut être très prudent à ce sujet, car on sait peu de choses de lui – imaginé d’une part une rotation de Vénus et de Mercure autour du soleil, afin d’expliquer leurs variations d’éclat ; mais surtout, il considérait que la voute céleste était fixe, et que c’était la terre qui était animée d’un mouvement de rotation autour de son axe sur une durée de 24 h ; le mouvement des étoiles n’était donc qu’une illusion. Si cela est vrai, Héraclide serait le précurseur de l’héliocentrisme et du système de Tycho Brahé au XVIe s.
Aristote (384-322 av. J-C)
Sur Aristote, voir ici.
La cosmologie d’Aristote
Aristote s’est intéressé à toutes les sciences de son temps, et notamment à l’astronomie et à la cosmologie, dans le Traité du Ciel, et dans les Météorologiques.
D’une part, il reprend à son compte la théorie d’Eudoxe de Cnide, mais à la différence de celui-ci, il considère les sphères comme des réalités concrètes. Il contribue en cela à la domination quasi sans partage du géocentrisme pendant plus de mille ans.
Aristote divise l’univers en deux parties : d’une part le monde sublunaire – le nôtre – soumis au changement et à la corruption, et d’autre part le monde supralunaire, celui du ciel et des astres, infini, inchangé, d’essence divine car constitué d’éther, le « cinquième élément » (les quatre autres étant l’air, l’eau, le feu et la terre).
D’autre part, il étudie la Terre elle-même, qu’il considère comme une sphère, et ce pour des raisons pratiques :
- La matière ayant tendance à tomber vers un centre commun, il en résulte que la Terre est sphérique ;
- lors des éclipses de lune, l’ombre de la terre sur la lune est sphérique ;
- si, lorsqu’on voyage vers le Sud, de nouvelles étoiles apparaissent, c’est parce que l’on circule à la surface d’une sphère.
Il estime sa circonférence à 400 000 stades, soit environ 60 000 km, ce qui est beaucoup plus que la réalité. Il la divise en cinq zones climatiques correspondant à l’inclinaison des rayons du soleil : deux zones polaires, deux zones tempérées habitables de chaque côté de l’équateur et une zone centrale à l’équateur rendue inhabitable en raison de la forte chaleur qui y règne.
Aratos de Soles (315-245 av. J-C)
Sans doute le plus célèbre des astronomes aujourd’hui, grâce à ses Phénomènes… qui, grâce à Cicéron, à Germanicus et finalement à Aviénus, devint un véritable phénomène d’édition !
Sur Aratos, voir ici.
Callippe de Cyzique (vers 370- vers 310)
Callippe, disciple d’Eudoxe, dont il a perfectionné le système des sphères, a calculé, à un jour près, la durée exacte des saisons, en 330 av. J.-C.
Il inventa, vers -331, un cycle à la fois lunaire et solaire de 76 ans. Ce cycle compte 441 mois creux (de 29 jours) et 499 mois pleins (30 jours), soit 441×29 + 499×30 = 27 759 jours, soit une année de : 27 759/76 = 365,25 jours.
Ce cycle, qui commença le 28 juin 330 av. J.-C., est appelé « période calippique ». Il fut adopté par l’ensemble du monde grec, y compris l’Asie conquise par Alexandre.
Le IIIe s. : Aristarque de Samos, Ératosthène de Cyrène
Aristarque de Samos (310-230 av. J-C)
Nous n’avons conservé que peu d’écrits de cet astronome et mathématicien qui vécut une grande partie de sa vie à Alexandrie, contemporain de Callimaque et d’Apollonios de Rhodes, mais nous connaissons sa théorie originale par l’Arénaire d’Archimède. Selon lui, le soleil, ainsi que les étoiles, sont immobiles ; c’est donc la Terre qui tourne, selon un double mouvement de rotation :
- autour de son axe, en une journée ;
- autour du Soleil, en une année.
Aristarque est donc, à notre connaissance, le premier à avoir élaboré un modèle héliocentrique. Mais il ne fut guère écouté car son hypothèse, d’une part était contraire à l’intuition (nous voyons le Soleil et les étoiles tourner autour de nous), et d’autre part soulevait des difficultés insurmontables à son époque. Alors que la théorie géocentrique supposait un univers relativement restreint, dont la sphère des étoiles constituait la limite, le système héliocentrique suppose un cosmos démesuré, dont les limites dépassent non seulement les capacités d’observation, mais même l’entendement. Et par ailleurs, l’on ne pouvait comprendre – il faudra attendre Galilée puis Newton pour cela – qu’une terre en mouvement ne projette pas les objets terrestres dans l’espace par l’effet de la force centrifuge : la notion de gravité était inconnue.
La théorie d’Aristarque fut donc laissée de côté – mais on peut imaginer qu’elle resta inscrite quelque part dans un coin de la mémoire des astronomes…
Par ailleurs, Aristarque est connu pour avoir calculé les diamètres de la terre, du Soleil et de la lune au moyen de calculs géométriques ; les résultats obtenus sont à vrai dire assez imprécis, car ses calculs sont entachés d’erreurs. Il a du moins le mérite de prouver que l’Univers est mesurable.
Il aurait été l’inventeur de la scaphè.
Aristylle de Samos (? – v. 280 av. J-C) et Timocharis d’Alexandrie (320-260 av. J-C)
Aristylle, astronome peu connu, a travaillé à la Bibliothèque d’Alexandrie ; il serait l’auteur, vers -300, du premier catalogue d’étoiles avec Timocharis d’Alexandrie.
Ce dernier, cité par Ptolémée dans son Almageste, aurait participé à la rédaction du catalogue d’étoiles. Tous deux ont inspiré Hipparque.
Ératosthène de Cyrène (276-194 av. J-C)
Né à Cyrène, cité grecque de l’actuelle Libye, à l’époque sous la domination de l’Égypte des Ptolémées, Ératosthène se définit d’abord comme un homme libre : sa vie, dans une période particulièrement troublée, a été retracée dans un beau roman de Thierry Crouzet, Ératosthène, éditions l’Âge d’homme, 2014 (voir la bibliographie). Il étudie d’abord sous la direction du grammairien Lysanias, puis il quitte Cyrène pour Athènes, où il suit quelque temps l’école stoïcienne, et où il rencontre peut-être Zénon ; mais il se refuse à se limiter à une seule école philosophique, et il écrit un Contre les philosophes qui lui vaudra la haine de l’ensemble de ceux-ci.
Il part ensuite à Alexandrie, où Ptolémée III Évergète le nomme en 245 directeur de la Grande Bibliothèque, où il succède ainsi à Callimaque de Cyrène et à Apollonios de Rhodes. Il le restera jusqu’à sa mort en 194, sous Ptolémée V.
Tout comme il avait refusé de se limiter à une seule doctrine philosophique, il revendique un grand éclectisme dans ses recherches : il sera donc à la fois poète, philosophe, mathématicien, astronome, géographe, historien et lexicographe.
En matière d’astronomie (et de géographie, un domaine dont il est l’inventeur), il est connu pour avoir calculé la circonférence de la terre, en se fondant sur les travaux de ses prédécesseurs, tout en les dépassant par une intuition géniale.
Il part tout d’abord de l’intuition d’Aristarque : le Soleil est en fait plus gros que la Terre, et il en est très éloigné : ses rayons sont donc pratiquement parallèles entre eux. Il reprend aussi la tentative assez malheureuse de Dicéarque (375-285 av. J-C) qui avait abouti à un calcul de 300 000 stades égyptiens (le stade égyptien mesure 157, 50 m).
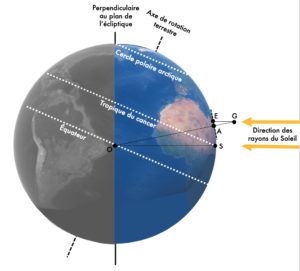
Sur l’illustration ci-contre, O est le centre de la Terre, S la ville de Syène, A celle d’Alexandrie, AG le gnomon installé à Alexandrie, AE l’ombre projetée par le gnomon sur le plan horizontal.
Ératosthène reprend le calcul à partir d’un fait : dans la ville de Syène, aujourd’hui Assouan, ville située sur le tropique du Cancer, au solstice d’été, à midi solaire, le soleil illumine brièvement le fond d’un puits – il est donc parfaitement à l’aplomb de la terre (sur l’illustration ci-dessus, O est le centre de la Terre, S la ville de Syène) ; or il en va différemment à Alexandrie (A sur l’illustration), qu’Ératosthène suppose sur le même méridien que Syène, ce qui est une approximation acceptable. Sur le schéma, AG représente le gnomon installé à Alexandrie, AE l’ombre projetée par le gnomon sur le plan horizontal.
Les angles SOA et AGE sont égaux puisque OS et EG sont parallèles. Ératosthène ayant mesuré l’angle AGE 1/50ème de 360°, il en déduit que l’angle SOA correspond à une distance SA, soit au 50ème de la circonférence de la Terre. D’où son estimation de 39 375 km pour la circonférence de notre planète, qui s’avère encore aujourd’hui comme une très bonne estimation, qui ne peut que confirmer que les mesures par Ératosthène de la distance SA – soit une distance de 5000 stades – et de l’angle AGE ont été faites avec beaucoup de rigueur.
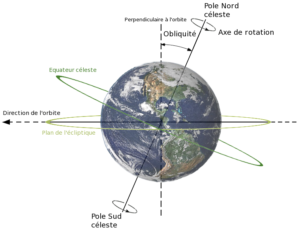
Description de l’inclinaison de l’axe de la Terre (obliquité) et son rapport aux plans de l’écliptique, à l’équateur céleste et à l’axe de rotation. La Terre est présentée telle que vue depuis le Soleil et la direction de son orbite est dans le sens inverse des aiguilles d’une montre (elle part donc vers la gauche).
Domaine public via Wikicommons.
Il aurait également calculé l’obliquité de l’écliptique, peut-être après Pythéas, dont il fut le premier à prendre le récit au sérieux.
Son œuvre la plus importante est les Catastérismes, dont il nous reste seulement un résumé. Bien qu’inspiré d’Aratos, ce n’est pas un catalogue d’étoiles, mais plutôt un travail mythographique, rappelant la transformation de héros ou d’objets en constellations.
Époque hellénistique et romaine
Hipparque (190-120 av. J-C)
il naquit vers 190 av. J-C à Nicée, en Bithynie (l’actuelle ville turque d’Iznik) ; il pratiqua ses observations astronomiques entre 147 et 127, à Rhodes et peut-être à Alexandrie. Il vécut encore quelques années, et mourut, sans doute en 120, à Rhodes.
Hipparque fut d’abord un mathématicien : il n’inventa peut-être pas la trigonométrie, mais rédigea les « Tables trigonométriques » ; il fut probablement aussi le premier Grec à utiliser des techniques arithmétiques chaldéennes ce qui lui permit d’améliorer les calculs des géographes et des astronomes.
Mais son œuvre principale concerne l’astronomie : il mesura avec une précision inégalée la position des astres, trouva une méthode pour prédire les éclipses lunaires, établit la distance de la terre à la lune, et découvrit la précession des Équinoxes : c’est grâce à ces découvertes qu’il rédigea son Catalogue d’Étoiles. Son rôle fut déterminant dans le développement d’une astronomie scientifique. Pline l’Ancien (23-79 apr. J.-C.) lui rend hommage dans son Histoire Naturelle (II, 24, 95)
Malheureusement, toute son œuvre disparut lors d’un incendie de la grande bibliothèque d’Alexandrie, à l’exception de son Commentaire sur les Phénomènes d’Eudoxe et d’Aratos. Le Catalogue d’étoiles, en particulier, ne subsistait plus que par une copie réalisée sur l’Atlas Farnèse ; c’est du moins ce que l’on croyait – jusqu’à ce qu’un chercheur, Peter Williams, directeur de la Tyndale House, examine au moyen de « l’imagerie spectrale de haute résolution » un palimpseste bien connu, et y découvre des coordonnées astronomiques. Mieux encore, les données exhumées, à savoir les positions des quatre étoiles les plus externes de la constellation de la Couronne Boréale, ont permis de déterminer, grâce à la précession des Équinoxes dont Hipparque fut précisément l’inventeur, de préciser à quelle date le texte avait été écrit : vers 129 av. J-C, c’est-à-dire au moment où notre astronome publia son Catalogue d’étoiles. Voir à ce propos l’article du Monde du 8 novembre 2022. Dans cet ouvrage, il répertorie 850 étoiles ; et il introduit une nouvelle notion, fondée sur la luminosité des étoiles : la magnitude, encore utilisée aujourd’hui. Les plus brillantes sont de magnitude 1, les plus faibles de magnitude 6.

L’Atlas Farnese, découvert dans les termes de Caracalla à Rome.
Domaine public via Wikicommons
Il découvrit la précession des Équinoxes : en comparant ses propres résultats à des catalogues du siècle précédent, notamment celui d’Aristylle de Samos et Philocharis d’Alexandrie, il s’aperçut que les étoiles avaient changé de place. Il en déduisit l’existence d’un mouvement général de la voute céleste. On découvrira plus tard que celui-ci est dû à la rotation de l’axe de la Terre.
Il serait l’inventeur de l’astrolabe : cet instrument, qui se fonde sur une projection plane de la voute céleste, permet de mesurer la hauteur des étoiles et du soleil.
Claude Ptolémée (100-168 apr. J-C)
Claude Ptolémée, dont le prénom, Claudius, indique qu’il est un citoyen romain, et le nom, devenu très courant au IIe s. apr. J.-C., qu’il était certainement un Grec d’Alexandrie. On ne sait rien de sa vie, qui se confond probablement avec ses recherches. Il est une exception dans un contexte relativement morose, tout comme Galien dans le domaine de la médecine.
Son œuvre astronomique, intitulée Composition mathématique ou Almageste (ἡ Μεγίστη, « la plus grande », avec l’article « al » d’origine arabe), est le seul ouvrage antique d’astronomie qui nous soit parvenu complet.
Il a survécu avec d’autres traités, les Hypothèses des planètes, le Tétrabiblos consacré à l’astrologie, ou encore la Géographie, ou encore des traités sur l’optique ou la musique. Outre ses propres recherches, il a eu le mérite de nous faire connaître ses prédécesseurs, qu’il cite abondamment, en particulier Hipparque.
Les instruments de l’astronomie grecque
Le premier instrument d’observation du ciel fut, naturellement… l’œil nu. Mais les limites de la vision naturelle s’imposaient d’elles-mêmes. Pourtant, si dès l’époque assyrienne, on fabriquait des lentilles avec du cristal poli, l’usage de ces lentilles pour améliorer la vision n’apparut qu’au Moyen-Âge. Quant aux lunettes astronomiques, permettant un grossissement significatif des objets, elles n’existèrent qu’à la fin du XVIe s. (lunette de Kepler) et au début du XVIIe s. grâce à Galilée.
C’est donc à l’œil nu que se pratiquaient les observations. Mais il existait d’autres instruments, permettant, eux, de se représenter les sphères célestes, et donc de se repérer parmi les constellations : d’abord les sphères (pleine, puis armillaire), puis l’astrolabe.
Les sphères, dont la sphère armillaire

Sphère armillaire de l’Encyclopédie de Diderot – domaine public via Wikicommons
L’astrolabe

Un astrolabe de Hartmann (1537) : domaine public via Wikicommons
La machine d’Anticythère
Bibliographie
Études générales
- Aujac Germaine, « Le ciel des fixes et ses représentations en Grèce ancienne« . In: Revue d’histoire des sciences, tome 29, n°4, 1976. pp. 289-307 ;
- Tannery Paul , Recherches sur l’histoire de l’astronomie ancienne, Paris, Georg Olms Verlag, 1976.
- Soubiran Jean, « Astronomie ancienne et technique moderne« . In: Pallas, 26/1979. pp. 3-10 ;
- Szabó Árpád, Maula Erkka, Les débuts de l’astronomie, de la géographie et de la trigonométrie chez les Grecs, Vrin, 1986 ;
- Szabó Árpád, L’aube des mathématiques grecques, Vrin, 2000, p. 9, 90 et 91.
- Cuisenier Jean, Le Périple d’Ulysse, éditions Fayard 2003, 451 p.
- Collectif, sous la direction de Christophe Cusset, Musa docta, Recherches sur la poésie scientifique dans l’Antiquité, Publications de l’Université de Saint-Étienne, 2006, 450 p.
- Crouzet Thierry, Ératosthène, éditions l’Âge d’homme, 2014, 453 p.
- Nazé Yaël, Astronomie du passé, de Stonehenge aux pyramides mayas, éditions Belin, 2018, 240 p.
- Pluchet Blandine, L’Astronomie pour les nuls, collection Vite et bien, éditions First, 2018, 415 p. ;
Textes anciens
- Aratos, Phénomènes, Éditions Les Belles-Lettres, collection Budé, traduction et commentaire de Jean Martin, deux tomes, 1998 ;
- Cicéron, Aratea, fragments poétiques, Éditions Les Belles-Lettres, collection Budé, traduction et commentaire de Jean Soubiran, 2002 ;
- Germanicus, Les Phénomènes d’Aratos, Éditions Les Belles-Lettres, collection Budé, traduction et commentaire d’André Le Boeuffle, 2002 ;
- Ptolémée, L’Almageste, traduction Pierre Paquette, 2022 ;
- Aviénus, Les Phénomènes d’Aratos, Éditions Les Belles-Lettres, collection Budé, traduction de Jean Soubiran, 2003 ;