Avant la naissance de la géographie : Homère

Les Grecs – et, avant eux, bien des peuples, notamment les Crétois, les Phéniciens, les Égyptiens… – n’avaient pas attendu l’avènement d’une géographie scientifique pour parcourir la terre et tenter de la connaître ; le témoignage le plus important pour la littérature occidentale est celui de l’Odyssée. L’on sait qu’Ulysse, après la guerre de Troie, voulut revenir à Ithaque, mais que des vents contraires l’empêchèrent de remonter vers le Nord après le cap Malée ; il dériva alors vers l’Ouest, jusqu’à pénétrer des contrées qui n’étaient plus celles des vivants…

Si l’on ne peut nier une large part mythique dans ce voyage, il constitue néanmoins un périple dont il est possible de retracer différentes étapes. Il fait partie d’un genre, celui des « récits de navigateurs » qui devaient former une large part du savoir géographique de l’âge archaïque.

Faute d’instruments de navigation et de cartes, les pilotes avaient en effet développé une exceptionnelle mémoire visuelle, et des connaissances empiriques fondées sur des « amers » (ces repères terrestres, arbre remarquable, éperon rocheux, anses… visibles du large), l’observation des courants, des vents, de la couleur de la mer, du vol des oiseaux, et, dès que le temps le permettait, des astres, et enfin de la vitesse de leurs navires. Ils se transmettaient ces informations dans des récits mi-réalistes, mi-fantastiques, souvent cryptés (les routes maritimes étaient l’objet d’une concurrence féroce) …

De nombreux navigateurs modernes ont tenté de reconstituer le périple d’Ulysse : Victor Bérard, Alain Bombard, et plus récemment Jean Cuisenier… Mais leurs conclusions divergent, en particulier pour la partie la plus occidentale du voyage ; la connaissance de la Terre restait donc floue, et imprégnée de légendes. Une vraie géographie restait à construire.

Premiers essais : Anaximandre et Hécatée de Milet

Il ne subsiste aucun ouvrage décrivant la Terre avant l’Empire romain ; fort heureusement pour nous, le géographe Strabon d’Amasée (63 av. J.-C.-23 apr. J.-C.), dans les deux premiers livres de sa Géographie, nous livre de larges résumés critiques de ses prédécesseurs : pour nombre d’entre eux, il constitue notre seule source.

Pour les Grecs du VI^e s. av. J.-C., la Terre était une grande inconnue : ce qu’on en savait se limitait à l’Oikoumène, c’est-à-dire la terre habitée : en gros, le pourtour de la Méditerranée, une partie de l’Afrique du Nord, l’Égypte, l’Empire perse, et la mer Noire… C’est-à-dire, en somme, tous les lieux que les Grecs avaient colonisé, ou bien où ils avaient établi des comptoirs. Quant à se la représenter au moyen d’une carte, c’était une autre affaire : pour établir les distances, on ne disposait guère que des données des voyageurs (jours de marche ou de navigation), et de quelques repères astronomiques, calculés notamment grâce au gnomon, utilisé par les Égyptiens et les Babyloniens. Il n’y avait aucune loi mathématique permettant de situer précisément les lieux décrits : nos parallèles et méridiens n’existaient pas encore, et les notions de longitude et de latitude étaient inconnues.

Si les récits des navigateurs, depuis Homère, et surtout depuis la grande vague de colonisation des VII^e et VI^e s. et l’intensification du commerce en Méditerranée avaient permis de se faire une idée de contrées jusqu’alors inconnues, un autre problème venait compliquer la représentation de la Terre : les mesures n’étaient pas universelles, mais différaient d’un lieu à un autre. Ainsi, le stade olympique valait 190 m, le stade égyptien (utilisé après la fondation d’Alexandrie en 332) 158 m. Or ce point était rarement précisé…

Première tentative de cartographie : Anaximandre de Milet (610-546)

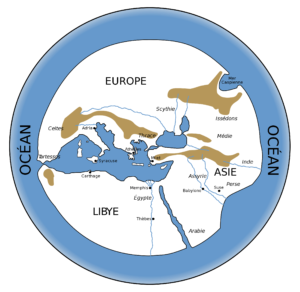
C’est à Anaximandre de Milet que l’on devrait, si l’on en croit Aristote, la première carte représentant la terre.

Aux yeux du philosophe, la Terre n’est pas nécessairement sphérique : il se la représente plutôt comme un cylindre, entouré, comme le dit la légende, par le fleuve Océan. La plus grande partie du monde est encore totalement inconnue. Quant à la dimension de notre planète, il l’évalue à 1/28^e de celle du Soleil (dans la réalité, le Soleil a environ 110 fois le diamètre de la Terre).

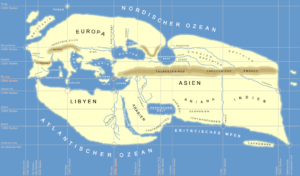
Seconde tentative : Hécatée de Milet (550-475)

Homme politique et géographe, né à Milet en 550, il écrivit une Périégèse ou « Tour de la Terre » décrivant l’ensemble de l’oikoumène, en se fondant sur la carte d’Anaximandre, mais en la complétant grâce aux récits des voyageurs. On voit qu’elle est plus détaillée et qu’y figurent les villes les plus importantes, même si l’on relève de grossières erreurs : le pourtour de la Méditerranée est à peu près connu, ainsi que l’Égypte jusqu’à Syène (Assouan) et la première cataracte, la Mésopotamie et une partie de l’Empire perse ; en revanche, l’Europe est à peu près inexplorée, tout comme l’Afrique, et la plus grande partie de l’Asie.

La connaissance de la Terre relève encore de l’empirisme, voire de la légende : ainsi du fleuve Océan entourant la terre de toute part. On a pu calculer que le monde connu couvre l’équivalent actuel de 17° de latitude, soit 6 fuseaux horaires sur 1/4 de l’hémisphère Nord, de Gibraltar à l’Indus, du cours inférieur du Dniepr à la première cataracte du Nil. Quant à la taille totale de la Terre, elle restait très approximative.

IV^e s. av. J.-C. : le choc des conquêtes d’Alexandre

Les conquêtes d’Alexandre

Les conquêtes d’Alexandre ont considérablement accru les connaissances géographiques en direction de l’Orient, et tout particulièrement de l’Inde. La découverte de celle-ci, et ses ressemblances troublantes avec l’Égypte – mêmes crues dévastatrices, mais en même temps fertilisantes, d’un grand fleuve, ici le Nil, là-bas le Gange, même population dont une partie était noire… fascinèrent les contemporains.

Mais Alexandre n’eut que le temps d’étendre son empire vers l’Est : l’occident resta à peu près inconnu.

De nouveaux centres de recherche : Alexandrie, Pergame…

Avec la dislocation de l’empire d’Alexandre, et l’émergence de nouveaux royaumes, le centre de gravité se déplace : Athènes, qui reste cependant un centre intellectuel important, n’est plus au centre du monde ; d’autres cités prennent le relais, se dotant de bibliothèques et attirant les savants de tout le monde grec : Pergame, et surtout Alexandrie.

De l’astronomie à la géographie : vers une connaissance scientifique de la Terre

Si l’astronomie a pu être décrite comme « la science des repères », capable de définir l’inclinaison de l’axe du monde, le tracé des cercles fondamentaux – l’équateur, les deux tropiques, le zodiaque – ainsi que la position, sur la sphère céleste, des principaux astres, notamment grâce aux travaux d’Eudoxe de Cnide et de ses successeurs, il n’en était pas encore de même de la géographie au IV^e s. Notre planète restait, pour une grande part, une inconnue. Les savants grecs étaient bien évidemment dans l’incapacité de l’observer de l’extérieur, et d’établir avec certitude à la fois sa place dans le cosmos (était-elle au centre de l’Univers ?), sa forme – en réalité la théorie de sa sphéricité était déjà bien ancrée, confortée par l’expérience des marins qui observaient depuis toujours la courbure de l’horizon – et sa dimension. L’on ne disposait, pour la mesurer, que des moyens des arpenteurs (mais il était difficile de mesurer de très grandes surfaces ou distances) et les récits des voyageurs : on mesurait en jours de marche ou de navigation, et l’on calculait les surfaces en prenant pour base la partie d’un champ labourée en une journée.

Les progrès conjoints des mathématiques et de l’astronomie vont permettre d’introduire une véritable observation scientifique de notre planète.

Les apports des astronomes et mathématiciens

Eudoxe de Cnide  (408 (?) -355 (?) av. J.-C.)

L’œuvre considérable d’Eudoxe en matière de calcul astronomique lui a aussi permis de poser les principes d’une cartographie mathématique, qu’il expose notamment dans trois ouvrages : Les Phénomènes (Τὰ Φαινόμενα), le Miroir (Τὸ Ἔνοπτρον) et le Circuit de la Terre (Ἡ περίοδος τῆς γῆς). Il part de deux principes :

1. L’axe de la Terre se confond avec l’axe du monde, et la Terre est le centre immobile de la sphère céleste. On sait que cette théorie ne sera abandonnée qu’après Galilée…
2. Tous les rayons du Soleil tombent parallèlement sur la surface terrestre.

Grâce à l’observation de l’étoile Canope (aujourd’hui α Carinae de la Constellation Argo) au moment du solstice d’été, il établit qu’à Cnide, sa ville natale, sur la côte de Carie, non loin de Rhodes, celle-ci rasait l’horizon, tandis qu’à Héliopolis, sur le delta du Nil, elle se trouvait au-dessus de l’horizon. Cette différence lui permit de calculer l’écart en latitude entre les deux villes. Ces calculs ont permis une première approximation de la circonférence terrestre, soit 240 000 stades.

Si l’on en croit Hipparque, Eudoxe serait également parvenu à calculer la latitude de la Grèce continentale, en utilisant le procédé gnomonique, ainsi que celui de Cyzique, située sur le même méridien que Cnide et où il a dirigé une école philosophique. À partir de ses recherches, on considéra la cité de Cnide comme le climat de référence.

Pythéas (IV^e s. av. J.-C.)

Astronome et explorateur né à Marseille, Pythéas est l’auteur d’un, ou peut-être deux ouvrages : De l’Océan, et Voyage (ou Périple) autour de la Terre, dont il ne reste que des fragments. Il aurait passé les Colonnes d’Hercule, contourné l’Espagne, remonté jusqu’en Grande-Bretagne, dont il aurait estimé le périmètre avec une relative justesse, avant de s’aventurer peut-être jusqu’en Islande (l’île de Thulé). Il serait l’un des premiers à identifier le phénomène des marées, quasi inconnu en Méditerranée, mais très puissant après les colonnes d’Hercule, et à le mettre en relation avec les phases de la Lune.

À l’aide d’un gnomon, il calcula avec précision la latitude de Marseille à 43°13′ – 2300 ans plus tard, on la définit à 43°18′, soit seulement 5′ de différence. Il remarqua également qu’à Marseille, au Solstice d’été, l’ensoleillement était de 15 h ; il en déduisit que toute ville présentant le même ensoleillement à la même date devait se trouver à la même latitude, donnant par la même occasion à la notion de « climat » une coloration météorologique.

Le double apport d’Eudoxe et de Pythéas permet de récolter des données plus nombreuses : on s’achemine vers une cartographie plus scientifique de la Terre.

Dicéarque de Messine (milieu du IV^e s. – 285 ou 280 av. J.-C.)

Disciple d’Aristote et adversaire de Théophraste, Dicéarque, qui privilégiait la vie active et engagée à la vie contemplative, fut aussi historien et géographe. Il identifia le parallèle du 36°N, qui joint les Colonnes d’Hercule au golfe d’Issos (Alexandrette, aujourd’hui Iskenderun) en passant par Rhodes : Ératosthène reprendra sa découverte, et fera de Rhodes le centre de sa carte.

Ératosthène, « inventeur » de la géographie

Ératosthène reprend donc le calcul de Dicéarque, situant Rhodes sur le 36e parallèle ; il cherche également à établir le méridien d’origine, passant par cette même île, en traçant une ligne partant au Nord vers le Bosphore et le Borysthène (aujourd’hui le Dniepr), au Sud vers Assouan et Méroé : c’est aujourd’hui le méridien 38°Est de Greenwich. Comme le souligne Didier Marcotte dans son article,

« C’est la première esquisse, à l’échelle de l’œkoumène, d’un système de représentation géométrique de l’espace, l’ancêtre de nos réseaux de coordonnées terrestres. » (art. cit. p. 17)

Si le gnomon permettait de calculer la latitude, et donc de tracer des parallèles – la bande horizontale entre deux parallèles est alors appelée « climat » (κλίμα) – il était beaucoup plus compliqué de déterminer la longitude, et donc de définir les méridiens. On pouvait le faire, ponctuellement, grâce aux éclipses de lune : si deux observateurs notaient le même phénomène, en deux lieux différents, il y avait autant de fois 1/24^e de cercle qu’il y avait d’heure de différence entre les deux. Par exemple, si un observateur X notait l’éclipse à 22 h, et un observateur Y la voyait, lui, à 0 h, il y avait donc deux heures d’écart, soit 2/24^e de cercle = 360/12 = 30°, soit à peu près 2900 km. Dans la pratique, on se bornait le plus souvent aux récits des voyageurs et des marins.

Posidonios d’Apamée (135-51 av. J.-C.)

Posidonios d’Apamée est surtout connu comme philosophe stoïcien, disciple de Panétius, ayant créé une école à Rhodes fréquentée par Cicéron et Pompée. Mais il fut aussi astronome et géographe. On lui doit l’établissement de la notion de parallèle : cercle abstrait reliant plusieurs points situés à la même latitude. Ayant remarqué que l’étoile Canope rasait l’horizon à Gadeira (Cadix) comme à Rhodes et à Cnide, il en déduisit que cette ville du Sud de l’Espagne était à la même latitude que ces deux villes.

Hipparque de Nicée (190-120. av. J.-C.)

Hipparque fut l’un de ceux, avec Ératosthène, qui prirent au sérieux le récit de Pythéas. En se fondant sur celui-ci, il établit le système de mesure des latitudes encore utilisé de nos jours. Si l’on considère que la sphère céleste mesure 360°, on peut la diviser en parallèles séparés chacun d’un degré, de l’équateur aux pôles. Le tropique du Cancer est donc à 24° Nord, le cercle de l’Ourse (ou cercle polaire) à 66° Nord – c’est la latitude de Thulé. Toujours en se fondant sur le récit de Pythéas, voici le tableau qu’il en tira (voir Barry Cunliffe, Pythéas, p. 120) :

	Hauteur du soleil en coudées	jour le plus long en heures	Distance en stades vers le Nord depuis Massalia	Latitude
Thulé		21-22		66°
Shetland	< 3	19	9100	61°
Lewis	4	18		58°
Île de Man	6	17	6300	54°
Trégor	9	16	3800	48°
Marseille		15,5		43°

Naissance de la notion de « climat »

Une notion purement géographique

Pour les premiers géographes « scientifiques », Eudoxe, Pythéas, Ératosthène, le « climat » se définit comme une bande horizontale, de largeur variable, et parallèle à l’équateur, comprise entre deux latitudes. Hipparque reprendra cette définition au II^e s. apr. J.-C. : pour lui, un climat = 1/360^e de cercle, soit, ramené à la circonférence de la Terre calculée par Ératosthène, 700 stades égyptiens, 124 km. Pour l’hémisphère Nord, au méridien de Méroé, il y a donc 90 climats.

Strabon reprendra le calcul d’Hipparque, mais en se limitant aux 14 parallèles les mieux connus. Or il note que 7 d’entre eux ont un écart d’ensoleillement de 30 minutes au solstice d’été : il définira donc 7 climats :

1. Méoé : 13 h d’enseoleillement
2. Syène : 13 h 30
3. Basse-Égypte : 14 h
4. Rhodes : 14 h 30
5. Hellespont : 15 h
6. Milieu du Pont : 15 h 30
7. Embouchure du Borysthène (Dniepr) : 16 h.

Une notion météorologique

L’on avait depuis longtemps noté qu’un déplacement de 400 stades, soit 70 km, en latitude (du Nord au Sud) suffisait pour remarquer un changement perceptible de climat, par exemple entre Athènes et Rhodes.

Depuis Parménide et surtout les Météorologiques d’Aristote, on savait distinguer 5 « climats », notion à la fois géométrique (il s’agit d’une « bande » parallèle à l’Équateur) et météorologique ; du Pôle Nord au Pôle Sud, on peut les énumérer ainsi :

1. Au-delà du cercle arctique, un climat glacial ;
2. Entre le cercle arctique et le Tropique du Cancer, une zone tempérée, habitable ;
3. Entre le Tropique du Cancer et le Tropique du Capricorne, à cheval sur l’Équateur, une zone brûlante, inhabitable ;
4. Entre le Tropique du Capricorne et le cercle antarctique, à nouveau une zone tempérée ;
5. Enfin, au-delà du cercle antarctique, une zone glaciale.

Cette théorie du climat témoigne donc de la rencontre entre la géométrie des cercles concentriques (latitudes) et l’étude du milieu, c’est-à-dire des conditions atmosphériques d’une latitude donnée, et de son influence sur les êtres vivants, développée notamment par les médecins qui établisssaient un lien entre le milieu et les maladies. Aristote, dans le Politique (VII, 1327b, 23-33) ira même plus loin, en associant le climat et les aptitudes politiques des peuples – une théorie qui connaîtra un énorme succès, jusqu’à Montesquieu :

« Τὰ μὲν γὰρ ἐν τοῖς ψυχροῖς τόποις ἔθνη καὶ τὰ περὶ τὴν Εὐρώπην θυμοῦ μέν ἐστι πλήρη, διανοίας δὲ ἐνδεέστερα καὶ τέχνης, διόπερ ἐλεύθερα μὲν διατελεῖ μᾶλλον, ἀπολίτευτα δὲ καὶ τῶν πλησίον ἄρχειν οὐ δυνάμενα· τὰ δὲ περὶ τὴν Ἀσίαν διανοητικὰ μὲν καὶ τεχνικὰ τὴν ψυχήν, ἄθυμα δέ, διόπερ ἀρχόμενα καὶ δουλεύοντα διατελεῖ· τὸ δὲ τῶν Ἑλλήνων γένος, ὥσπερ μεσεύει κατὰ τοὺς τόπους, οὕτως ἀμφοῖν μετέχει. καὶ γὰρ ἔνθυμον καὶ διανοητικόν ἐστιν· διόπερ ἐλεύθερόν τε διατελεῖ καὶ βέλτιστα πολιτευόμενον καὶ δυνάμενον ἄρχειν πάντων, μιᾶς τυγχάνον πολιτείας. »

« Les nations qui vivent dans les lieux froids, et ceux qui sont autour de l’Europe, sont pleins de courage, mais inférieurs en intelligence et en art, raison pour laquelle ils restent davantage libres, mais ils sont sans constitution et incapables de commander leurs voisins ; ceux qui habitent vers l’Asie ont l’âme intelligente et industrieuse, mais sans courage, c’est pourquoi ils sont commandés et réduits en esclavage ; quant à la nation des Grecs, se trouvant située entre les deux, participe des deux natures, et est à la fois courageuse et industrieuse ; c’est pourquoi elle est libre, parfaitement organisée et capable de conquérir l’univers, si elle se trouve sous un seul gouvernement. »

Cette théorie des climats prendra un caractère beaucoup plus systématique après la découverte, par les soldats d’Alexandre, du monde Indien. Celui-ci est situé à la même latitude que l’Égypte, et comme elle est traversée par un grand fleuve, là le Nil, ici le Gange, aux crues à la fois dévastatrices et fertilisantes ; mais il présente des différences irréductibles. Sur sa carte, Ératosthène représente l’Inde comme un losange, avec au Nord une chaîne de montagnes (l’Himalaya), immédiatement au Nord du parallèle de Rhodes. Il y a donc un climat spécifique à l’Inde.

La théorie des climats sera reprise et systématisée par les Stoïciens et surtout Posidonios d’Apamée (IIe – Ier s. av. J.-C.). Strabon en fait mention (II, 3, 7, C102).

Bibliographie

• Chevallier Raymond, « La géographie dans le monde antique », Revue des Études grecques,‎ janvier-juin 1976, pp. 115-116
• Marcotte Didier. « Entre Athènes et Alexandrie, la genèse de la notion de climat« . In: Vie et climat d’Hésiode à Montesquieu, Paris : Académie des Inscriptions et Belles-Lettres, 2018. pp. 89-118. (Cahiers de la Villa Kérylos, 29) ;