Claude Ptolémée, dont le prénom, Claudius, indique qu’il est un citoyen romain, et le nom, devenu très courant au II^e s. apr. J.-C., qu’il était certainement un Grec d’Égypte. Il n’a aucun lien de parenté connu avec la dynastie macédonienne des Ptolémée, qui gouverna l’Égypte de la conquête d’Alexandre à la mort de Cléopâtre. Il est né à Canope, dans le delta du Nil, sous le règne des Antonins, à l’apogée de l’empire, plus précisément sous le règne de Trajan (98-117). Il connut successivement quatre empereurs : Trajan, Hadrien, Antonin le Pieux et Marc-Aurèle. Il travailla probablement à la Grande Bibliothèque d’Alexandrie entre 127 et 141, puisqu’il y fit des observations astronomiques ; il mourut sans doute à Canope, sa cité natale.

On ne sait rien de sa vie, qui se confond probablement avec ses recherches. Il est une exception dans un contexte relativement morose, tout comme Galien dans le domaine de la médecine.

Son œuvre astronomique, intitulée Composition mathématique ou Almageste (ἡ Μεγίστη, « la plus grande », avec l’article « al » d’origine arabe), est le seul ouvrage antique d’astronomie qui nous soit parvenu complet. Il a survécu avec d’autres traités, les Hypothèses des planètes, le Tétrabiblos consacré à l’astrologie, ou la Géographie, ou encore des traités sur l’optique ou la musique. Outre ses propres recherches, il a eu le mérite de nous faire connaître ses prédécesseurs, qu’il cite abondamment, en particulier Hipparque. C’est à travers lui, dans ses traductions arabes et byzantines, que l’Occident médiéval prit connaissance de la science grecque.

L’astronomie de Claude Ptolémée : l’Almageste

Dans la lignée de Pythagore et de Platon, Ptolémée affirme la prééminence des mathématiques, qui sont le seul savoir inébranlable par la rigueur de ses démonstrations. C’est pour cette raison qu’il conserve l’idée de la sphère : la géométrie du cercle permet en grande partie de « sauver les apparences ». La Terre est donc sphérique, immobile au centre de l’Univers, car le plan de l’horizon coupe la sphère céleste en deux moitiés ; les cieux eux-mêmes sont sphériques. On voit là également l’influence d’Aristote : Ptolémée reprend l’idée d’un monde supra-lunaire fait d’éther, le plus homogène des éléments : or la surface des corps homogènes ne peut elle-même qu’être homogène, donc sphérique.

Si, comme Aristote, Ptolémée refusait d’envisager un mouvement de la Terre, c’est aussi parce que l’on considérait que l’observation confirmait ce que l’on savait de la physique : or on n’avait pas les moyens techniques qui auraient permis de détecter les effets de la rotation terrestre. Il faudra pour cela attendre le XVII^e s. et les travaux des académiciens de Florence, et surtout la deuxième moitié du XIX^e s. et le fameux pendule de Foucault…

Comme ses prédécesseurs, Ptolémée voulait expliquer les mouvements irréguliers des corps célestes en termes de combinaisons de mouvements circulaires uniformes, sur le modèle des épicycles et des excentriques défini par Apollonios de Pergè. Il donne ainsi une théorie du Soleil, et montre que ces deux modèles sont équivalents ; il préfère en ce cas la seconde explication, plus simple.

En plus de ses travaux théoriques, Ptolémée réalisa un prodigieux travail d’observation : il reprend le catalogue d’Hipparque, qui contenait déjà 850 étoiles ; il parvient, lui, à en identifier 1028. Il utilise pour cela l’astrolabe armillaire (à ne pas confondre avec l’astrolabe plan) pour déterminer avec précision les positions de la lune : il construisit sans doute son propre instrument. Cependant, lorsque son modèle mathématique, rationnellement satisfaisant, entrait en conflit avec l’observation – ainsi, selon sa théorie, la distance de la Terre à la Lune aurait dû varier du simple au double, ce qui n’est pas exact – il préférait la théorie. Son seul objectif était de fournir un modèle géométrique permettant de calculer les mouvements de la Lune, des planètes et du Soleil. Par des observations et des calculs, il parvint à donner un exposé systématique de chacune des planètes, en calculant la grandeur de son épicycle, son excentricité, et des tables permettant de calculer la position longitudinale de la planète, ainsi que la grandeur et la durée des rétrogradations de chaque planète. Cette théorie pouvait être critiquable – et fut critiquée par Copernic – mais constitua l’essentiel des savoirs astronomiques jusqu’à la Renaissance.

Ptolémée peut être considéré comme le dernier astronome grec : ses théories devinrent rapidement un véritable dogme, qui ne sera remis en question qu’à partir du XVI^e s. avec Tycho Brahé. Il représente donc à la fois l’apogée de l’astronomie grecque, et son chant du cygne.

L’Almageste

L’Almageste, dont le titre grec était Μαθηματική σύνταξις, est le seul traité d’astronomie complet qui nous soit parvenu. On peut prendre connaissance en ligne de cet ouvrage dans une nouvelle traduction française de Pierre Paquette, datée d’avril 2022. Avant lui, il n’existait en français que la traduction de Nicolas Halma, datée de 1813-1815, reprise par Jean Peyroux en 1988.

Le livre est constitué de 13 livres :

1. Forme de la Terre ; exposés de concepts mathématiques ;
2. La Terre et les différentes données qui la concernent : pôles, écliptique, équateur, méridiens…
3. Le Soleil et ses mouvements ;
4. La Lune et ses mouvements ;
5. L’astrolabe ; le calcul des mouvements de la Terre et du Soleil ;
6. Les éclipses ;
7. Les étoiles fixes ;
8. Les étoiles fixes ;
9. Les sphères du Soleil, de la Lune et des cinq planètes ; Mercure ;
10. Vénus et Mars ;
11. Jupiter et Saturne ; la longitude des cinq planètes ;
12. Les rétrogradations des cinq planètes ;
13. La latitude des cinq planètes ; épilogue.

L’astrologie selon Ptolémée

Outre l’Almageste, Ptolémée est aussi l’auteur du Tétrabiblos, consacré à l’astrologie, c’est-à-dire l’influence des astres sur le monde sublunaire, et sur les destinées individuelles des hommes. Cela peut nous surprendre ; mais bien plus tard encore, Copernic, Tycho Brahé, Kepler et même Newton croyaient aussi en l’astrologie…

En outre, Ptolémée se montre relativement prudent et rationnel : il s’intéresse notamment à l’influence du Soleil sur les saisons, ou à celle de la Lune sur les marées…

La Géographie de Ptolémée

Carte de Ptolémée

Claude Ptolémée ne fut probablement pas un grand voyageur, mais plutôt un homme de cabinet, capable de connaître et de synthétiser l’ensemble des connaissances de son temps. Sa Géographie compte parmi ses œuvres majeures, couvrant l’ensemble de la terre habitée (l’Œkoumène) connue à son époque. Elle est composée de huit livres :

• Livre I : définition du sujet ; données et méthodes utilisées ;
• Livres II à VII : listes topographiques et coordonnées de plus de 8000 lieux, allant de l’Irlande et de la Grande-Bretagne à l’Inde, en passant par l’Allemagne, l’Italie, la Grèce, l’Afrique du Nord, l’Asie mineure et la Perse ;
• Livre VIII : 26 cartes régionales (10 pour l’Europe, 4 pour l’Afrique (qu’il appelle « Libye », et qui reste le grand continent inconnu) et 12 pour l’Asie.

Les sources de Ptolémée

Ptolémée s’appuie sur les travaux de Dicéarque, de Posidonios d’Apamée et de Marinos de Tyr, un Romain d’origine phénicienne qui reprit le système de coordonnées géographiques de Dicéarque. Mais, alors que Marinos estime l’étendue de la Terre habitée était de 225° de l’Espagne à la Chine (au lieu des 130° véritables), il reprend l’estimation de Posidonios pour la circonférence du globe au lieu de celle, plus exacte, d’Ératosthène : Ptolémée gardera cette estimation, mais recalculera plus exactement les dimensions de l’Œkoumène.

La géographie

Ptolémée choisit donc de considérer la Terre comme une sphère de 180 000 stades (33 345 km), qu’il divise, selon le système sexagésimal babylonien, en 360° de longitude, de 500 stades chacun (soit 92,625 km) – aujourd’hui, un degré représente 111,319 km à l’équateur. Pour lui, qui ignore bien sûr le méridien de Greenwich, le méridien de longitude zéro se situait au point le plus occidental alors connu, à savoir les « Îles Fortunées », autrement dit les Canaries.

La latitude, dont le degré zéro est, comme aujourd’hui l’Équateur, s’étend de Thulé, le point le plus septentrional connu (63°N) jusqu’à Agisymba, qu’il situe à 8200 stades au Sud de l’Équateur, soit environ 1500 km, en Afrique sub-saharienne (16°S). L’ensemble couvre donc, de Thulé à Agisymba, 79°.

Dans cette zone délimitée par les latitudes et longitude, Ptolémée définit une partie habitable, de 72000 stades (13 338 km) en longitude sur 40000 en latitude (7410 km) (98 834 580 km²).

Ptolémée va surtout établir les coordonnées géographiques précises de plus de 8 000 lieux, en se fondant sur les travaux de ses prédécesseurs, et des récits de voyageurs.

La cartographie

Ératosthène avait, le premier, établi des cartes de géographie fondées sur des données scientifiques ; Hipparque avait amélioré ses calculs. Ptolémée, en se fondant sur les travaux mathématiques d’Euclide (vers 300 av. J.-C.), améliore la projection de la sphère sur une surface plane.

Postérité de Ptolémée

La Géographie de Ptolémée constitue une somme des connaissances accumulées au II^e s. apr. J.-C. ; il en est aussi la fin, au moins jusqu’à la Renaissance : il n’y aura guère de nouveautés jusqu’aux « Grandes Découvertes« .

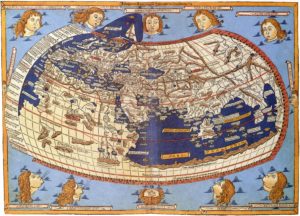
Le livre a été longtemps considéré comme perdu ; il fut redécouvert par le Byzantin Maximus Planudes vers 1300. Il était cependant connu des Arabes, qui l’avaient traduit. On pense que les cartes figurant aujourd’hui dans l’ouvrage datent non de l’époque de Ptolémée, mais de l’époque byzantine.

Vers 1410, il sera l’une des sources du cosmographe Pierre d’Ailly, dans son Imago Mundi, qui inspira lui-même Christophe Colomb : celui-ci en possédait un exemplaire.